Hello Potato World
[포테이토 스터디] LRP: Layer-wise Relevance Propagation 본문
⋆ 。 ˚ ☁︎ ˚ 。 ⋆ 。 ˚ ☽ ˚ 。 ⋆
[XAI study_ Interpretable Machine Learning]
20210802 XAI study 발표자료 (참고블로그주소 References)
LRP: Layer-wise Relevance Propagation

LRP : 분해를 통한 설명(Explanation by Decomposition)을 통해 Neural Network의 결과물을 이해할 수 있게 도와주는 방법
input x가 총 d차원으로 이루어져있다고 하면, d차원의 각각의 feature들이 최종 output을 도출하는데에 서로다른 영향력을 가지고 있다고 가정하고 이 기여도(Relevance Score)를 계산하여 분석하는 방법이다.

- $x$ : sample image
- $f(x)$ : 이미지 x에 대한 prediction "Rooster"
- $R_i$ : prediction $f(x)$를 얻기 위해 이미지 x의 각 pixel들이 기여하는 정도(각 차원의 Relevance Score)
- LRP의 결과 heatmap : 이미지 x의 각 pixel들의 Relevance Score를 색깔로 표시
=> 오른쪽 상단(수탉의 부리나 머리)을 보고 x에 대한 prediction을 "Rooster"로 출력했다는 것을 알 수 있다
Intuition & Mathematically
2-1. Intuition
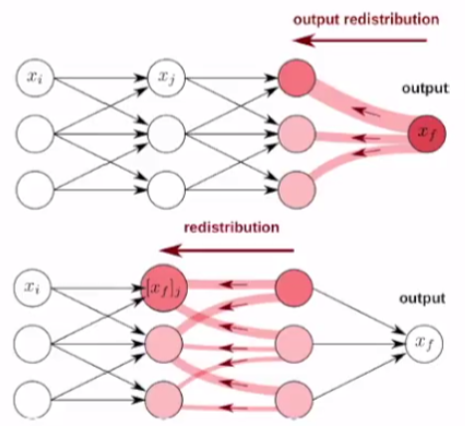
LRP: Layer-wise Relevance Propagation (Top-down)
: Relevance score를 Output layer에서 Input layer 방향으로 계산해나가며 그 비중을 재분배하는 방법
- 모든 Neuron은 각각의 기여도(Certain Relevance)를 가지고 있다
- Relevance는 Top-down 방식으로 재분배
- 재분배시 Relevance는 보존된다
(ex) "Rooster"의 prediction 확률이 0.9였다고 한다면, Neuron들에 Relevance score를 재분배한 후에 각 layer에서의 relevance score의 합은 0.9로 보존되어야 한다.
2-1. Mathematically

Deep Neural Network의 prediction($f(x)$)를 수학적으로 분해하고, Certain Relevace를 정의할 방법
=> 각 Neuron의 input과 output의 관계 이용
(Relevance Score : input의 변화에 따른 출력의 변화 정도)
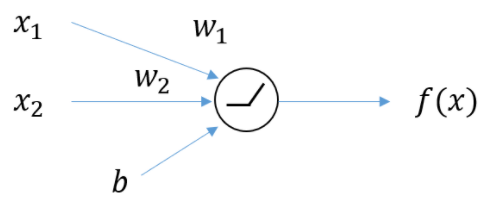
2차원 입력(2weights, 1bias)을 갖는 Neuron
$y=f(x)=f(x_1,x_2)$
x값의 변화에 따른 $f(x)$의 변화량을 통해 Relevance Score를 예측하기 위해 미분(변화량) 이용
output $f(x)$에 대한 각각의 입력 $x_1, x_2$의 기여도 표현
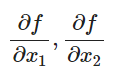
위와 같이 표현된 $x_1, x_2$의 기여도와 $f(x)$의 관계를 설명할 수 있는 식을 도출할 수 있는 Taylor Series 도입
Taylor Series
Taylor Series : 어떤 점에서 무한 번 미분가능한 함수를 그 점에서 미분계수 값으로 계산할 수 있는 무한급수로 표현된 함수

2차 이상의 미분계수의 항들을 error($\epsilon$)으로 설정하여 First-order Taylor Series로 나타내면

위의 예시에서 input은 $x_1, x_2$이므로(실제 Neural Network에서는 더 복잡한 다변수) 다변수 함수의 Taylor급수 이용
2-dimension에서의 Taylor급수 예시

마찬가지로 error term을 이용해 나타낸 First-order Taylor Series

Middle term이 Relevance score를 결정하고, x의 변화에 따른 $f(x)$의 변화를 알 수 있다
불필요한 Term인 $f(a)$와 $\epsilon$을 없애기 위해 0으로 근사
- $f(a)=0$
- ReLU 활성화함수 특성을 이용해 $\epsilon=0$으로 근사

ReLU 특성을 이용한 $\epsilon=0$
예시로 사용한 그림과 같이 2개의 input $x_1, x_2$를 갖는 Neuron의 ReLU 함수
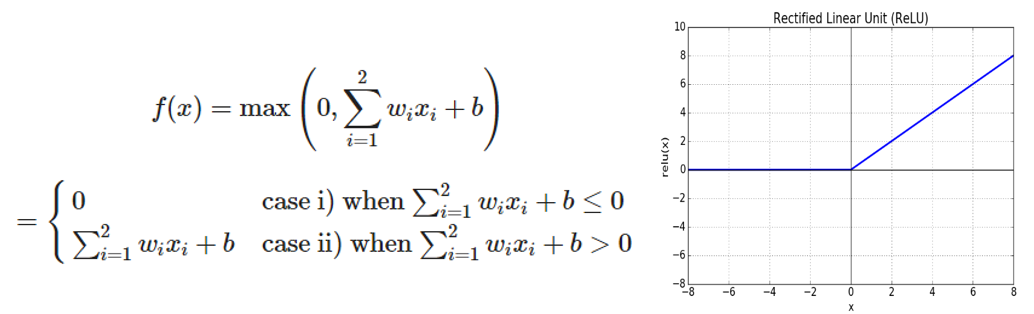
- case 1 : 이미 0의 값을 가지므로 변형X
- case 2 : Taylor급수로 표현

Taylor급수로 표현한 식을 $f(x)$의 weight 표현과 비교하면 $w_1, w_2$를 $x_1, x_2$각각에 대한 1차 편미분 값으로 표현할 수 있다는 것을 볼 수 있다
2차 이상의 편미분 계수는 모두 0으로 나오기 때문에(기울기 변화 없는 ReLU의 특성), 2차 이상의 미분으로 표현한 $\epsilon$의 값이 0이 되는것을 알 수 있다
=> 𝜖=0

$f(a)=0$을 만드는 a를 찾는 방법

하나의 Neuron에서, 두 개의 입력값 $x_1, x_2$과 ReLU 통과 후의 출력값을 도식화한 그림 (입출력의 관계)
- 흰색에 가까울수록 0에 가깝고 빨간색에 가까울수록 큰 값
- 실선표시 지점 : 모든 값이 0인 지점
- 점선표시 지점 : 동일한 값을 갖는 등고선
$w^2$-rule을 사용하여 a값 구하는 방법
그림에서의 화살표 vector표현(관계)

$f(a)=0$을 만드는 a를 구하기 위해 해당 제약조건을 만들면

구해진 t값을 사용해 다시 벡터 x를 표현하면 (a = x+tw에 대입)

따라서 $f(x)$를 재정의하면 ($f(x)$표현식에 a대입)

$w^2−rule$외에 $z−rule, z^+−rule$등 다른 기법도 사용하여 a값을 구할 수 있다
Relevance Propagation Rule

적절한 a를 찾음으로써 하나의 Neuron의 출력 $f(x)$를 분해

위에서 다룬 각 Neuron에서의 계산 방법을 전체 Neural Network에 적용
- Forward Pass : input $x_p$에 대한 Neural Network의 최종 output $x_f$
- Relevance Propagation : 각 Neuron이 가지는 Relevance Score $R_f$를 $x_f$와 동일하게 설정한 다음 계속해서 Top-down 계산 수행
=> Neural Network상의 모든 Neuron들의 Relevance Score를 계산할 수 있게 된다.
Decomposition
Decomposition : input의 각 feature가 결과에 얼마나 영향을 미치는지 해체하는 방법
(ex) Image x를 "cat"으로 분류하는데 각 hidden layer에서 계산한 기여도를 토대로 해당 input image x의 feature들이 모델을 어떻게 받아들였는지 히트맵으로 도식화
- Positive 영향을 준 feature : 빨강
- Negative 영향을 준 Feature : Blue
=> 이마, 코, 입 주변의 pixel들이 결과에 영향을 많이 준 것을 확인할 수 있다
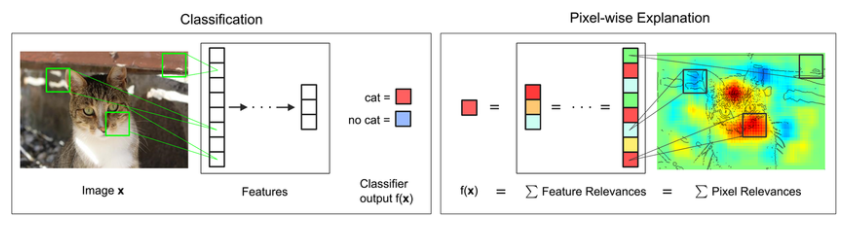
따라서 LRP는 Relevance Propagation과 Decomposition방법을 사용해 모델을 해부하는 방법이다
Image Application Example
LRP는 Image, Text 데이터 등에 다양하게 적용될 수 있다.
(Image Classification 모델에 LRP를 적용한 결과)


References
[1] Explaining NonLinear Classification Decisions with Deep Taylor Decomposition, Montavon et al., 2015
[2] XAI 설명 가능한 인공지능, 인공지능을 해부하다, 안재현, 2020
[3] https://angeloyeo.github.io/2019/08/17/Layerwise_Relevance_Propagation.html
'Study > XAI' 카테고리의 다른 글
| [포테이토 스터디] Detecting Concepts (0) | 2021.06.28 |
|---|---|
| [포테이토 스터디] Pixel Attribution (Saliency Maps) (0) | 2021.06.28 |
| [포테이토 스터디] Influential Instances (0) | 2021.06.22 |
| [포테이토 스터디] Prototypes and Criticisms (0) | 2021.06.22 |
| [포테이토 스터디] Local Surrogate(LIME) (0) | 2021.05.24 |




