Hello Potato World
[포테이토 스터디] Influential Instances 본문
⋆ 。 ˚ ☁︎ ˚ 。 ⋆ 。 ˚ ☽ ˚ 。 ⋆
[XAI study_ Interpretable Machine Learning]
6.4 Influential Instances
머신러닝 모델은 Training Data로 학습된 결과물이기 때문에 하나의 Training Instance를 삭제하는 것은 결과 모델에 영향을 준다.
- Influential Training Instance
해당 instance의 삭제가 모델의 "Parameters"또는 "Prediction"에 상당한 변화를 주는 Data
머신러닝 모델을 "Debug"하거나, Prediction을 "Better Explain"할 때 유용할 수 있다.
- Outlier
Dataset의 다른 Instance들과 멀리 떨어져 있는 Instance
거리(ex. Euclidean Distance)측정을 통해 멀리 떨어진 Instance
1-d Gaussian 분포를 따르는 아래 Data에서 x=8인 data가 outlier

- Influential Instance
제거했을 때 학습된 모델에 큰 영향을 미치는 Instance
모델 재학습 시 Parameters 또는 Prediction의 변화가 클수록 Instance의 영향이 큼

Full Data를 사용했을 때와 Influential Instance를 제거했을 때 각각 학습된 Linear Model의 기울기 변화
: x=8의 instance가 기울기에 큰 변화를 주기 때문에 Influential instance라고 할 수 있다.
- Influential Instance가 모델 해석에 주는 이점
Key Idea : 모델의 Parameter와 Prediction이 시작된 위치, 즉 Training Data를 거꾸로 추적하는 것
- Training Data : Features X + Target y
- Learner : Training Data로부터 Model을 학습
- Model : 새로운 데이터에 대한 Prediction 도출

Training Process에서 Intancs가 제거됐을 경우 모델의 Parameter나 Prediction이 어떻게 변화하는지 측정
모델이 고정된 PDP나 Feature Importance의 방법과 대조된다
- 2가지 범위의 Influential Instance
- 모델 Parameter나 Prediction에 전체적으로 가장 영향을 크게 미친 Influential Instance
- 특정 Prediction에 가장 영향을 크게 미친 Influential Instance
- Two Approaches
- Deletion Diagnostics
- Influence Functions
6.4.1 Deletion Diagnostics
1. DFBETA
Instance의 삭제가 모델의 Parameter에 주는 영향 측정
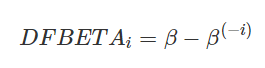
- β : 모든 Data를 사용해 학습된 모델의 weight 벡터
- β(-i) : i번째 Instance를 제거하고 재학습된 모델의 weight 벡터
weight parameter가 존재하는 Model에만 적용 가능 : Logistic Regression, Neural Networks ....
2. Cook's Distance
Instance의 삭제가 모델의 Prediction에 주는 영향 측정
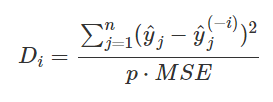
- 분자 : i번째 Instance를 포함했을 때와 안 했을 때의 prediction의 Squared Difference
- 분모 : Feature의 개수 p와 전체 MSE의 곱 (모든 Instance에 대하여 동일)
weight parameter는 필요 없지만, MSE를 사용하기 때문에 모든 종류의 모델에 사용할 순 업음(ex. Classification)
=> 두 가지 방법 모두 각 Instance를 삭제할때마다 모델 재학습 필요
6.4.2 Influence Functions
모델을 재학습할 필요 없지 않고, Training loss를 통해 Instance들의 가중치를 높여 모델이 얼마나 변화할지 근사하는 방법

- 매우 작은 값 ε만큼 z의 가중치 증가
- θ는 가중치 부여 전후 모델의 parameter vector
- L은 학습된 모델의 Loss function
- 𝑧𝑖는 Training Data, 𝑧z는 가중치를 높일(removal simulation) Training Instance
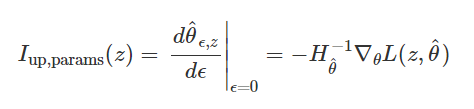
Hessian Matrix와 Loss Gradient의 곱으로 표현된다.
- Loss Gradient
모델의 parameter가 바뀌었을 때 Loss가 얼마나 바뀔지 gradient의 변화 추정
- Positive entry : parameter가 증가하면 모델의 loss 증가
- Negative entry : parameter가 증가하면 모델의 loss 감소 - Hessian Matrix
모델의 parameter에 관한 2차 미분값을 행렬로 표현한 것
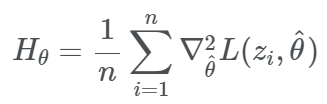
- Intuition
Loss를 정확히 계산할 수 없기 때문에 Parameter 주위의 2차 확장 형성

현재 설정된 Parameter에서 경사도(기울기)와 곡률(Hessian Matrix)의 정보를 사용하여 새 Parameter의 근사치를 계산
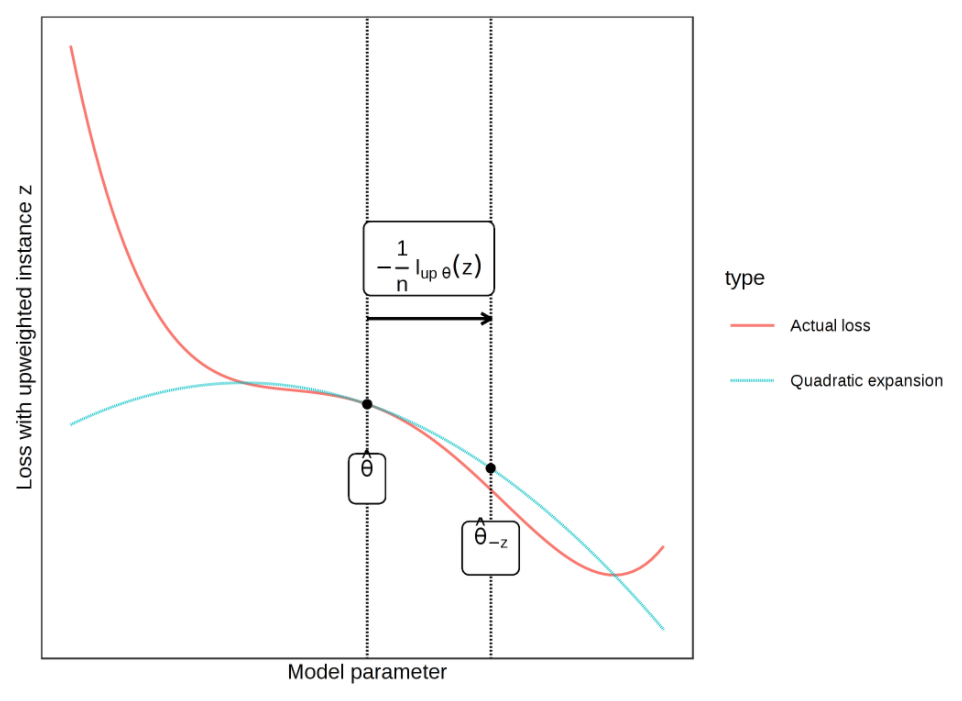
z를 삭제할 때 Loss가 정확하게 어떻게 계산될지는 그래프(Actual loss: 그림에서 붉은색 그래프)를 추정하기 어렵지만, 2차 확장(Quadratic expansion: 그림에서 민트색 그래프)을 형성하여 2차 근사치를 작성하고 Loss 추정
- 새로 계산된 Parameter를 사용하여 Prediction에 미치는 영향 계산할 수 있음 (Chain Rule 사용)

- 첫번째 줄 : Instance z의 가중치를 높여 계산된 새 parameter로 예측된 z(test)에 대한 Loss function의 변화를 통해 영향력 계산
- 최종식이 의미하는 바 : "parameter의 변화에 따른 instance의 변화 정도"와 "z의 가중치를 높였을 때 parameter의 변화 정도"의 곱
Applicants of Influence Functions
1. Understanding model behavior
머신러닝 모델마다 예측 방법이 다름
같은 Prediction이 나오더라도 시나리오는 다름
어떤 Instance에 가장 영향을 받았는지를 분석하여 feature를 파악할 수 있다.
2. Handling domain mismatches / Debugging model error
- Domain Mismatch : Training과 Test의 Data분포가 다른경우
예를들어, 하나의 병원에서 수술을 받은 환자들의 Data로만 training한 후에 다른 병원에서 수술을 받은 환자의 Data로 prediction하는 경우, Training과 Test의 Data분포가 다르기 때문에 예측은 틀릴 수 있음.
예측을 실패한 새 Instance를 선택하여 가장 영향력 있는 Instance를 골라냈을 때,
예측 실패 Instance : 고령의 노인 / Influential Instances : 젊은 환자들
이라면 "나이"라는 feature에 의해 영향을 크게 받음을 알 수 있다. 따라서 다양한 나이대의 Data를 더 수집하여 학습하는 등의 해결책을 제시할 수 있다.
3. Fixing Training Data
Training Data의 validation 횟수에 제한이 있을 때, Training Data중에서 Random으로 고르거나/ 영향력이 없는 Outlier들을 포함해서 선택하는 것보다 가장 영향력 있는 Data들을 선택하여 검증하는 게 더 좋은 selection이다.
6.4.3 Advantages
- Training Process에서의 Training data의 영향을 직접 강조하기 때문에 머신러닝 모델을 위한 최고의 Debugging Tool이 될 수 있다.
- Model-agnostic으로, 모델의 종류에 상관없이 사용가능
- 따라서 여러 머신러닝 모델을 비교할 수 있음
6.4.4 Disadvantages
- 모든 Training Data를 제거하여 각각 모델을 재학습해야하기 때문에 계산비용이 매우 큼
- Influential Funciton이 좋은 대안이 될 수 있지만, parameter와 loss function을 계산할 수 있는 모델에 한해서만 적용할 수 있음
- Influential Function은 근사화를 하는 도구일 뿐, 정확한 값이라는 보장이 없음
- Influention Instance와 Non-Influential Instance로 구분하는 뚜렷한 cutoff가 없음
References
[1] Interpretable Machine Learning, Christoph Molnar
'Study > XAI' 카테고리의 다른 글
| [포테이토 스터디] Detecting Concepts (0) | 2021.06.28 |
|---|---|
| [포테이토 스터디] Pixel Attribution (Saliency Maps) (0) | 2021.06.28 |
| [포테이토 스터디] Prototypes and Criticisms (0) | 2021.06.22 |
| [포테이토 스터디] Local Surrogate(LIME) (0) | 2021.05.24 |
| [포테이토 스터디] Global Surrogate (1) | 2021.05.24 |




