Hello Potato World
[포테이토 스터디] Prototypes and Criticisms 본문
⋆ 。 ˚ ☁︎ ˚ 。 ⋆ 。 ˚ ☽ ˚ 。 ⋆
[XAI study_ Interpretable Machine Learning]
6.3 Prototypes and Criticisms
- Prototypes이란, 모든 데이터를 대표하는 data instance
- Criticisms란, Prototypes의 세트로 잘 표현되지 않는 data instance
Prototypes와 Critisms은 Data를 설명하기 위해서도 사용되지만, Interpretable model을 만들거나 Black box 모델을 Interpretable하게 만들 때 사용될 수 있다.
- Simulated Data Distribution
Prototypes과 criticisms는 항상 데이터 내의 instances중 하나로 선택된다.
(아래 그림에서 마름모가 prototype으로 선택된 instance, 동그라미가 criticism으로 선택된 instance이다.)

- Data에서 Prototype을 찾는 방법
1. K-medoids
K-means와 연관된 클러스터링 알고리즘
- Prototypes
Cluster의 centroid를 prototype으로 선택 - Criticisms
prototypes만 찾아낼 수 있고, criticisms은 찾지 못함
2. MMD-Critic
전체 Data의 분포와 선택된 Prototypes의 분포를 비교하여 차이를 최소화하는 방법
단일 framework로 prototypes과 criticisms 둘 다 찾아내 줄 수 있음
- Prototypes
Prototypes의 분포가 원래 Data의 분포와 가장 비슷할 수 있도록 선택
다른 Data cluster 내에 있는 경우 Data가 많이 밀집되어 있는 영역의 Data point가 좋은 prototype - Criticisms
선택된 Prototypes가 잘 설명하지 못하는 영역 내의 Data point를 Criticisms로 선택
6.3.1 MMD-Critic Theory
- MMD-Critic Procedure
- 찾고싶은 Prototypes와 Criticisms의 개수 지정
- Prototypes를 Greedy Search를 통해 선택. Data의 분포와 Prototypes의 분포가 최대한 가까울 수 있도록 선택
- Criticisms를 Greedy Search를 통해 선택.Data의 분포가 Prototypes의 분포와 다른 영역의 Point 선택
- MMD-Critic에 필요한 것들
1. Kernel Function
Kernel : 두 개의 Data Point 사이를 근접성에 따라 가중치를 주는 Function
2. Maximum Mean Discrepancy (MMD)
Kernel Function(K)를 사용하여 두 분포간의 차이를 측정
kernel을 통한 두 점 사이의 근접성 계산의 합을 통한 분포 비교
- MMD-critic의 목표 : Minimizing MMD^2
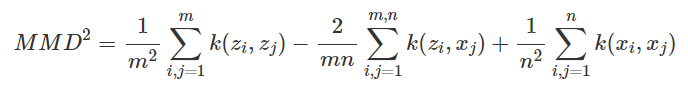
(z : 선택된 Prototypes, x : 원래 data에 있는 Data Points)
- 첫번째 Term : 모든 Prototypes 사이의 평균 근접도
- 세번째 Term : 모든 Data Points 사이의 평균 근접도
- 두번째 Term : 선택된 Prototypes와 모든 Data Points 사이의 평균 근접도 (최소화를 위해 가장 중요한 Term)
- MMD^2 측정의 예시
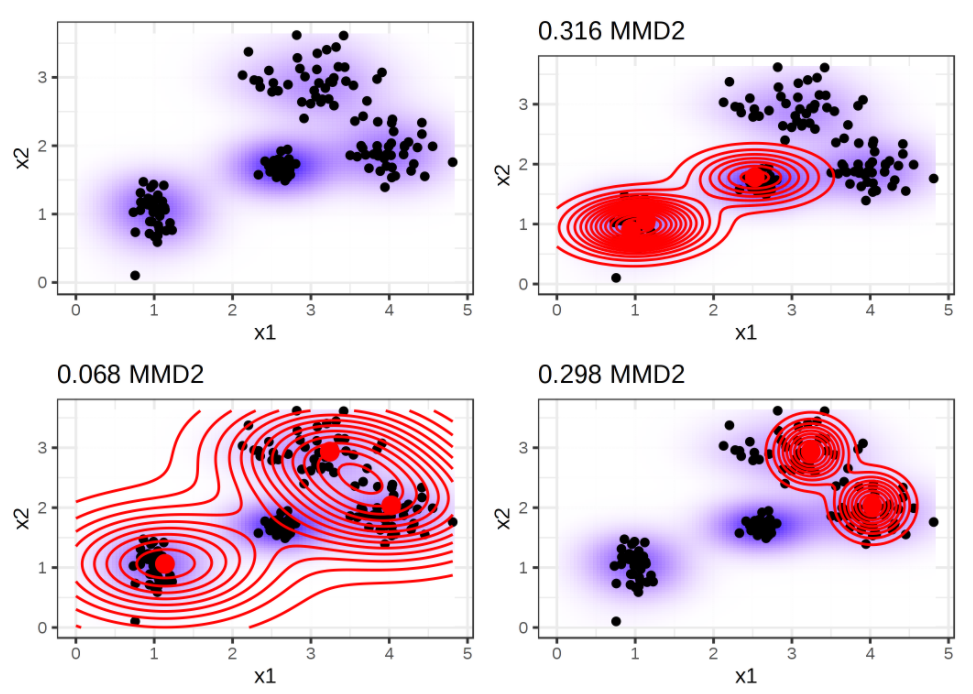
- 첫번째 그림 : 원래 Data의 분포
- 나머지 그림 : 다양하게 선택된 Prototypes와 같이 계산된 MMD^2의 측정치
3번째 그림이 가장 낮은 MMD^2값 보임
(3번째 그림에서 빨간색으로 표시된 Prototypes의 분포가 원래 Data의 분포에 가장 근접한 모습을 볼 수 있음)
- Choice of Kernel(예시. radial basis function kernel):
두 점 사이의 Euclidean 거리와 scaling parameter를 사용하여 근접도 계산

- Prototype을 찾기 위한 Greedy Search
- 빈 prototype list 생성
- 각각의 Data를 순서대로 prototype list에 추가해서 MMD^2를 계산한 후에 이 값을 최소화 하는 Prototypes를 m개 선택(m은 지정된 값)
- Prototype list 반환
- Witness Function
특정 point x에서의 두 분포가 얼마나 다른지 측정하는 함수
- 첫번째 Term : 점 x와 Data들 사이의 평균 근접도
- 두번째 Term : 점 x와 Prototypes들 사이의 평균 근접도
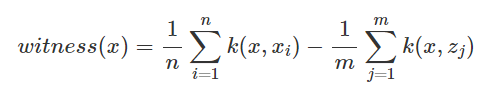
- 값이 0에 가까울수록 Data Point x에서의 두 분포는 비슷함
- Witness 값이 Negative이면 : 두번째 Term이 더 크기 때문에 Prototypes가 필요 이상으로 선택됨(Overfitting)
- Witness 값이 Positive이면 : 두번째 Term이 더 작기 때문에 Prototypes가 Data의 분포를 나타내기에 부족(Underfitting)
- 수동으로 선택된 여러 Data Point에서의 Witness Function Value (Evaluation)

6.3.2 Example
Handwritten Digit Dataset에 MMD-critic을 적용한 예시
아래 그림은 Dataset에서 선택된 Prototypes를 시각화한 자료이다.

- 각 숫자 당 이미지 수가 다름
- 클래스 당 고정된 개수가 아니라 전체 데이터셋에서 고정된 수의 Prototype이 선택되었기 때문
6.3.3 Advantages
- (어떤 연구에서) 새로운 이미지 한장을 받아 주어져있던 두 개의 이미지 중 하나의 class로 구분해야 하는 실험에서, Random Image가 아니라 Prototype의 이미지를 받았을 때 더 잘 구분해냈음
- Prototypes와 Criticism의 개수를 마음대로 설정할 수 있음
- Data의 분포만을 사용하기 때문에, 어떤 Dataset이나 머신러닝 모델에 적용될 수 있음
- 알고리즘 구현이 쉬움
- Criticisms의 선택은 Prototypes의 선택과 무관 (MMD-critic 제외)
6.3.4 Disadvantages
- Criticism의 선택은 Prototypes의 선택에 크게 좌지우지함
- Prototypes와 Criticisms 개수를 직접 설정해줘야 함
- Kernel의 종류나 Kernel scaling 매개변수를 선택하는 방법이 명확하지 않음
References
[1] Interpretable Machine Learning, Christoph Molnar
'Study > XAI' 카테고리의 다른 글
| [포테이토 스터디] Pixel Attribution (Saliency Maps) (0) | 2021.06.28 |
|---|---|
| [포테이토 스터디] Influential Instances (0) | 2021.06.22 |
| [포테이토 스터디] Local Surrogate(LIME) (0) | 2021.05.24 |
| [포테이토 스터디] Global Surrogate (1) | 2021.05.24 |
| [포테이토 스터디] Permutation Feature Importance (0) | 2021.05.22 |




