Hello Potato World
[포테이토 논문 리뷰] Siamese Contrastive Embedding Network for Compositional Zero-Shot Learning 본문
[포테이토 논문 리뷰] Siamese Contrastive Embedding Network for Compositional Zero-Shot Learning
Heosuab 2023. 1. 8. 18:02⋆ 。 ˚ ☁︎ ˚ 。 ⋆ 。 ˚ ☽ ˚ 。 ⋆
[Zero-shot learning paper review]
Compositional Zero-shot Learning (CZSL)
인간은 이미 알고 있는 개체에 대한 정보들을 조합하고 구성하여 새로운 개체에 일반화하는 능력을 가지고 있다. 다시 말해서, 이미 알고 있는 "whole apple"과 "sliced banana"의 정보를 조합해서 새로운 개체인 "sliced apple" 또는 "whole banana"를 생각해낼 수 있다. 이 능력을 AI 시스템에서 모방하고자 하는 task를 Compositional Zero-shot Learning (CZSL)이라고 한다.

CZSL에서는 각각의 개체(composition)을 두 가지의 구성 요소, state와 object로 분해한다. "whole", "sliced"처럼 개체의 상태를 표현하는 요소는 state, "apple", "banana"처럼 개체의 형태와 종류를 구분짓는 요소는 object로 정의된다. CZSL의 목표는 Training data와 test data가 공통 원소를 가지지 않고 분리되어 있다는 가정 하에, 새로운(unseen) test composition을 식별하는 것이다.
State와 object를 모두 식별하기 위해 CZSL에서 사용하던 대표적인 방법으로는,
- 두 가지의 classifier를 따로 두어 state와 object를 따로 학습하는 구조를 사용할 수 있다. 하지만 이 방법은 state-object 사이의 상호 작용 또는 entanglement를 무시하게 된다.
- 또 모든 composition과 visual feature들이 한번에 투영될 수 있는 공통 embedding space를 학습하여 embedding 사이의 거리를 계산하여 활용하는 방법이 있는데, training과 test composition 사이의 차이를 무시하여 비슷한 개체들을 혼동할 수 있다. (e.g., young cat and young tiger)
따라서 해당 논문에서는 state와 object 각각의 구분적인 prototype를 활용하지만 둘 사이의 joint representation도 함께 학습하는 Siamese Contrastive Embedding Network (SCEN)을 제안한다.
Siamese Contrastive Embedding Network (SCEN)
States의 집합을 $A$, objects의 집합을 $O$라고 하면, state-object의 쌍으로 구성되는 components의 집합 $C$는 다음과 같이 표현될 수 있으며,
\[ C = A \times O = \{(a,o) \mid a \in A, o \in O\} \]
Training dataset에서의 images 집합을 $I^s$, 그에 대응하는 component를 $C^s$ ($C^s \subset C$) 라고 하면, image-component의 쌍으로 구성되는 training dataset $D_{tr}$은 다음과 같이 표현된다.
\[ D_{tr} = \{((i,c) \mid i \in I^s, c \in C^s\} \]
CZSL task의 정의에 따라 training data와 test data는 공통 원소를 가지지 않아야 하기 때문에, training data의 composition을 $C^s$, test data의 composition을 $C^u$라고 한다면 $C^s \cap C^u = \emptyset$을 만족해야 한다. 또한 새로운 이미지를 seen, unseen composition 중에서 예측해야 하기 때문에, $\{I^s, C^s\}$로 학습된 mapping function $I \to C^s \cup C^u$를 학습하는 것을 목표로 한다.
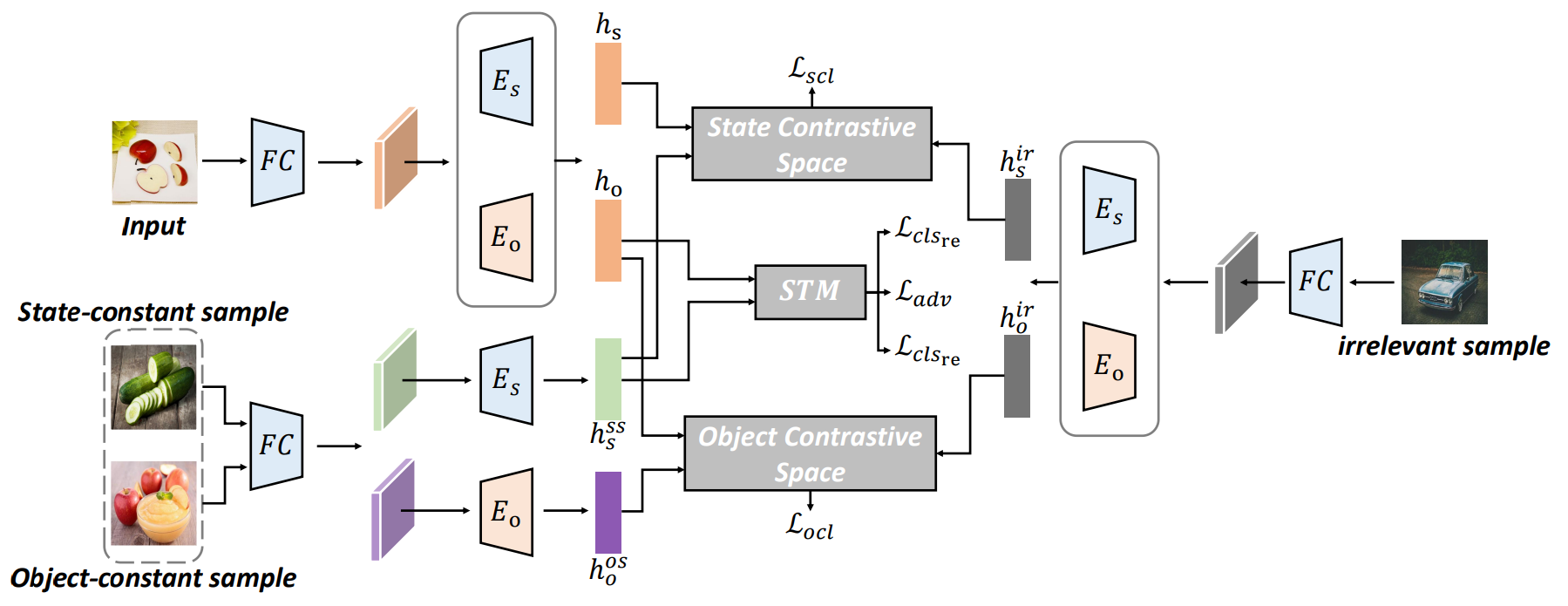
SCEN 구조를 세 가지 모듈로 요약하면,
- Encoding : states와 objects 각각의 encoding
- Contrastive learning : state/object 각각의 contrastive space에서의 prototypes 추출
- Augmentation : State Transition Module(STM)을 통해 가상의 composition 생성
- Module 1. Encoding
하나의 이미지가 feature extractor FC를 통과해서 얻은 visual feature $x$는, state/object 구성 요소로 분해하기 위해 두 개의 embedding으로 인코딩된다. State-specific Encoder $E_s$는 state를 잘 표현하기 위해, Object-specific Encoder $E_o$는 object를 잘 표현하기 위해 학습된다.
\[ h_s = E_s(x) \]
\[ h_o = E_o(x) \]
State-object의 다양한 조합을 통해 여러 composition을 구성할 수 있기 때문에, 이러한 joint representation을 학습하기 위해 세 가지의 데이터베이스를 정의한다.
- 고정된 state에 다양한 objects를 조합하는 State-constant database $D_s$
- 고정된 object에 다양한 states를 조합하는 Object-constant database $D_o$
- 다양한 objects-states 조합 중에서 input instance와 관련이 없는 Irrelevant database $D_{ir}$
state $\hat{a}$와 object $\hat{o}$로 이루어진 input instance $x=(\hat{a},\hat{o}) \in I^s$가 입력되면, 세 가지의 데이터베이스는 다음과 같이 구성된다.
\[ D_s = \{(a,o) \mid a=\hat{a}, (a,o) \in C^s\} \]
\[ D_o = \{(a,o) \mid o=\hat{o}, (a,o) \in C^s\} \]
\[ D_{ir} = \{(a,o) \mid a \ne \hat{a}, o \ne \hat{o}, (a,o) \in C^s \} \]
- Module 2. Contrastive learning
$E_s, E_o$를 통해 두 개의 독립된 embedding space (Siamese contrastive space)로 투영된 $h_s, h_o$는 contrastive learning을 통해 state와 object 각각을 가장 잘 표현할 수 있는 prototype으로 학습된다. 하지만 기존의 contrastive loss를 사용하여 state와 object를 따로 학습하면 state-object interaction이 무시되기 때문에, 정의된 세 가지의 데이터베이스를 사용하여 loss를 새로 정의한다.
- State-based contrastive loss $\mathcal{L}_{scl}$
input $x$의 state encoding $h_s$가 state-based contrastive space의 anchor로 설정된다. input $x$와 동일한 state를 가지는 데이터베이스 $D_s$로부터 positive sample $h_s^{ss}$을 추출하며, 동일하지 않은 state를 가지는 데이터베이스 $D_{ir}$로부터 $k$개의 negative samples $\{ h_{s_1}^{ir}, ..., h_{s_k}^{ir} \}$를 추출한다.
anchor와 positive 사이의 거리는 가까워지도록, anchor와 negative 사이의 거리는 멀어지도록 학습하는 contrastive loss는 다음과 같이 정의된다. ($\tau_s > 0$ : temperature parameter)
\[ \mathcal{L}_{scl} = -log \frac{exp((h_s)^{\top} h_s^{ss} / \tau_s)}{exp((h_s)^{\top} h_s^{ss}/\tau_s) + \sum\nolimits_{i=1}^K exp((h_s)^{\top} h_{s_i}^{ir}/ \tau_s)} \] - Object-based contrastive loss $\mathcal{L}_{ocl}$
object-based contrastive space의 anchor는 $h_o$로 설정된다. 동일한 object를 가지는 데이터베이스 $D_o$로부터 positive sample $h_o^{os}$를 추출하며, 동일하지 않은 object를 가지는 데이터베이스 $D_{ir}$로부터 $k$개의 negative samples $\{ h_{o_1}, ..., h_{o_k}^{ir} \}$를 추출한다.
state-object interaction을 고려하기 위해 $D_{ir}$로부터 추출하는 negative samples는 두 가지의 loss에서 동일한 데이터를 사용한다. ($\tau_o > 0$ : temperature parameter)
\[ \mathcal{L}_{ocl} = -log \frac{exp((h_o)^{\top} h_o^{os} / \tau_o)}{exp((h_o)^{\top} h_o^{os}/\tau_o) + \sum\nolimits_{j=1}^K exp((h_o)^{\top} h_{o_j}^{ir}/ \tau_o)} \] - Classification Loss $\mathcal{L}_{cls}$
Classifier가 state와 object 각각의 prototype을 통해 구별할 수 있도록, 두 공간에서의 classification loss를 독립적으로 계산한다. $C_a$ 와 $C_o$를 state와 object 각각에 대한 classification을 하는 fully connected layers라할 때, 전체 classification loss는 다음과 같다.
\[ \mathcal{L} = C_a(h_s, a) + C_o(h_o, o) \]
위에서 정의한 세 가지의 loss를 통해 Siamese Contrastive Space의 전체 loss $L_{cts}$가 정의된다.
\[ \mathcal{L}_{cts} = \mathcal{L}_{scl} + \mathcal{L}_{ocl} + \mathcal{L}_{cls} \]
- Module 3. Augmentation
Training data에 등장하지 않는 unseen composition에 대한 일반화 성능을 높임으로써 training과 test 사이의 차이를 줄이기 위해, 가상의 composition을 생성하는 State Transition Module (STM) 구조를 제안한다. STM은 Training data에 두 가지의 composition, "sliced apple", "red fox"가 있다고 했을 때, 데이터에는 없지만 실제로 존재할 법한 "red apple"을 생성하되, 데이터에도 없고 실제로도 존재하지 않는 "sliced fox"는 구별해내는 것을 목표로 한다.

- 입력 이미지의 object와 다른 이미지들의 다양한 state를 조합하기 위해 각각의 prototype을 얻는다. Object-specific encoder를 통해 input $x$의 object prototype $h_o$를 추출하고, state-specific encoder를 통해 다른 샘플 $\{ s_1, s_2, ..., s_n \}$의 state prototype $ h_{\tilde{s}} = \{ h_{s_1}, h_{s_2}, ..., h_{s_n} \}$를 추출한다.
- Generator $G$ 는 추출한 prototype을 조합하여 가상의 composition을 만든다.
\[ G(h_{\tilde{s}}, h_o) = \hat{x}_{\tilde{s},o} \] - Discriminator $D$ 는 생성된 가상의 composition 내에서 실제로 존재하지 않을만한 데이터 (irrational composition)을 판별한다.
\[ \underset{D}{max} \underset{G,E_s,E_o}{min} V(G, D) = \mathbb{E}_{s,o} (logD(x_{a,o})) + \mathbb{E}_{h_{\tilde{s}},h_o} (log(1-D(G(h_{\tilde{s}},h_o)))) \] - 새로 생성된 데이터로 $E_s$ 와 $E_o$ 의 성능을 높이는 것이 목적이지만, 생성된 이미지는 label이 없기 때문에 re-encode 과정을 거친다. 다시 인코딩 과정을 거쳐서 추출된 state/object prototype을 통해 학습하는 re-classification loss를 정의할 수 있다.
\[ \mathcal{L}_{cls_{re}} = C_a(E_s(G(h_{\tilde{s}}, h_o)), \tilde{a}) + C_o(E_o(G(h_{\tilde{s}}, h_o)), o) \]
위에서 정의한 두 가지의 loss를 통해 State Transition Module (STM)의 전체 loss $\mathcal{L}_{stm}$가 정의된다.
\[ \mathcal{L}_{stm} = \underset{D}{max} \underset{G,E_s,E_o}{min} V(G, D) + \mathcal{L}_{cls_{re}} \]
본 논문에서 제안한 SCEN framework의 final loss는 $\mathcal{L}_{cts}, \mathcal{L}_{stm}$의 weighted sum으로 정의된다.
\[ \mathcal{L}_{total} = \alpha \mathcal{L}_{cts} + \beta \mathcal{L}_{stm} \]
Results
CZSL의 대표적인 benchmark dataset 세 가지에서 실험 결과를 보인다 : MIT-States, UT-Zappos, C-GQA

MIT-States 데이터셋에서 test AUC score를 기준으로 했을 때 기존의 SOTA인 5.1%를 뛰어넘는 5.3% (+0.2%)를 기록했으며, Harmonic Mean(HM) score를 기준으로 했을 때 18.4% (+1.2%)를 기록했다. State와 object 각각에 대한 예측의 accuracy로 보아도, 28.2% (+0.3%)와 32.2% (+0.4%)의 최고 성능을 보인다. 마찬가지로 UT-Zappos에서도 SOTA performance를 기록하였다.

가장 최근 발표된 C-GQA 데이터셋에서도 AUC, HM, state/object accuracy 모두 향상된 결과를 보인다.
